1. 강의 자료
https://www.notion.so/teamsparta/2-9e5eccb6b7ce4c4ba028dae6ad135830
[스파르타코딩클럽] 알고보면 알기쉬운 알고리즘 - 2주차
매 주차 강의자료 시작에 PDF파일을 올려두었어요!
www.notion.so
2. 강의 듣기 전 계획과 생각


2주차 커리큘럼에는 면접에서도 자주 질문이 나오며, 여러가지 알고리즘에서 많이 사용하는 링크드 리스트와 배열에 대한 이야기들부터 이진 탐색과 나중에 배울 DFS, BFS에 사용되는 재귀함수까지 실려있었다.
3. 핵심 강의 내용
▶ 배열 : 크기가 정해진 데이터의 공간 (calloc, malloc) 으로, 한 번 정해지면 변경할 수 없음.
▶ 링크드 리스트 : 리스트는 크기가 정해지지 않은 데이터의 공간.
따라서 앞 뒤의 포인터만 변경하면 원소의 삽입/삭제를 O(1)의 시간 복잡도 안에 할 수 있음.

▶ 클래스 : 속성과 기능을 가진 객체를 총칭하는 개념.
▶ 이진 탐색 : 범위를 절반씩 줄여가며 탐색하는 탐색법.
☞ 시간 복잡도 : O(logN)

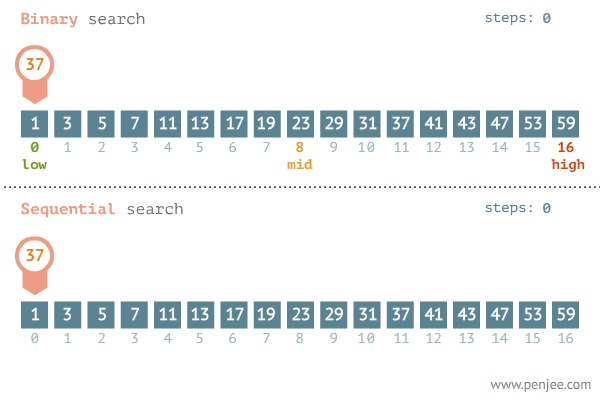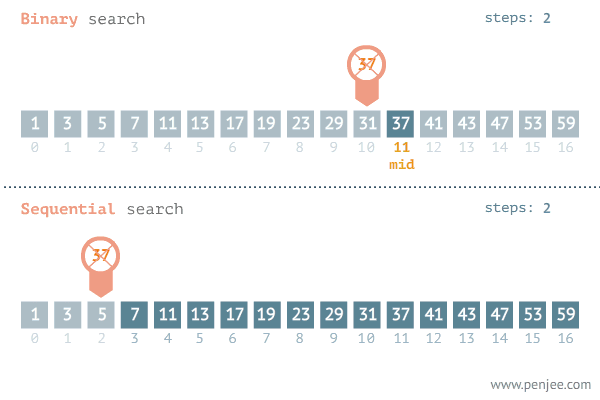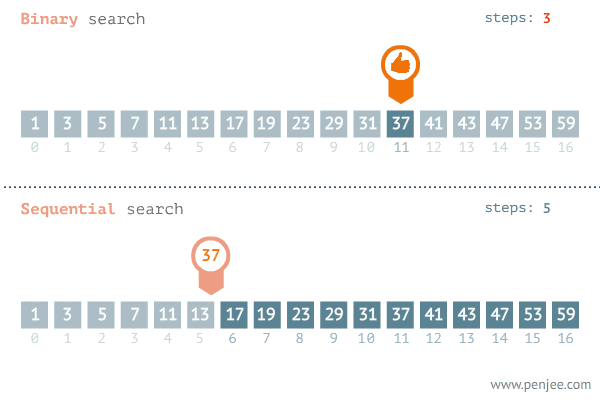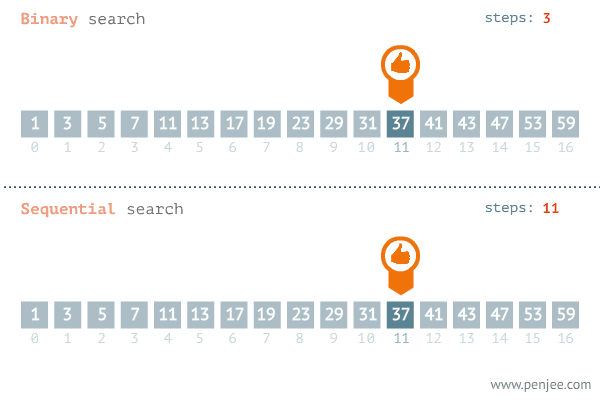
▶ 재귀 : 어떠한 것을 정의할 때 자기 자신을 참조하는 것을 뜻함.
Comment : C/C++ 위주로 공부했었기에 Python의 List 작동 원리에 대해 바로 의문이 들었었는데, 바로 설명 해주셔서 좋았습니다.
Internals of Python list, access and resizing runtimes
Is Python's [] a list or an array? Is the access time of an index O(1) like an array or O(n) like a list? Is appending/resizing O(1) like a list or O(n) like an array, or is it a hybrid that can ma...
stackoverflow.com
https://en.wikipedia.org/wiki/Dynamic_array
Dynamic array - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search List data structure to which elements can be added/removed Several values are inserted at the end of a dynamic array using geometric expansion. Grey cells indicate space reserved for e
en.wikipedia.org
4. 문제풀이
▶ 링크드 리스트 끝에서 K번째 값 출력하기
# 나의 풀이
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self, value):
self.head = Node(value)
def append(self, value):
cur = self.head
while cur.next is not None:
cur = cur.next
cur.next = Node(value)
def get_kth_node_from_last(self, k):
node_pointer = []
cur = self.head
while cur.next is not None:
cur = cur.next
node_pointer.append(cur)
return node_pointer[-k]
linked_list = LinkedList(6)
linked_list.append(7)
linked_list.append(8)
linked_list.append(9)
linked_list.append(10)
print(linked_list.get_kth_node_from_last(2).data) # 9가 나와야 합니다!]
# 튜터님 풀이
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self, value):
self.head = Node(value)
def append(self, value):
cur = self.head
while cur.next is not None:
cur = cur.next
cur.next = Node(value)
def get_kth_node_from_last(self, k):
length = 0
cur = self.head
cur_k = self.head
while length < k:
cur = cur.next
length += 1
while cur is not None:
cur = cur.next
cur_k = cur_k.next
return cur_k
linked_list = LinkedList(6)
linked_list.append(7)
linked_list.append(8)
linked_list.append(9)
linked_list.append(10)
print(linked_list.get_kth_node_from_last(2).data) # 9가 나와야 합니다!]Comment : 첫번째로 사용한 방법은 길이를 알고 그를 통해 값을 도출하는 방법입니다. 길이를 구하기 위한 탐색1번, 값을 도출하기 위한 탐색1번으로, 총 탐색횟수가 2번입니다.
두번째로 사용한 방법은 서로 길이 k만큼 떨어진 포인터 두 개를 두고, 한 칸씩 이동하는 방법입니다. 하나의 포인터가 리스트 끝까지 도달하기 위한 탐색1번으로, 총 탐색횟수가 1번입니다.
하지만 시간복잡도 측면에서 보면, 둘다 결국 링크드 리스트의 끝까지 가야 하므로 같은 O(N) 의 성능을 가지게 됩니다. 게다가, 생각해보면 두 개의 공간값을 가지고 이동해야 하므로 비슷하게 연산량을 사용합니다. 따라서 반드시 더 빠르다고는 할 수 없습니다.
▶ 배달의 민족 배달 가능 여부
shop_menus = ["만두", "떡볶이", "오뎅", "사이다", "콜라"]
shop_orders = ["오뎅", "콜라", "만두"]
#1 나의풀이 (이진 탐색)
def is_available_to_order(menus, orders):
menus.sort()
complete_cnt = 0
for order in orders:
pl = 0
pr = len(menus) - 1
pc = (pl + pr) // 2
while pl <= pr:
if menus[pc] == order:
complete_cnt += 1
break
elif menus[pc] > order:
pr = pc - 1
elif menus[pc] < order:
pl = pc + 1
pc = (pl + pr) // 2
if complete_cnt == len(orders):
return True
else:
return False
result = is_available_to_order(shop_menus, shop_orders)
print(result)
#2 나의 풀이 (in 연산자 활용)
def is_available_to_order(menus, orders):
for order in orders:
if order not in menus:
return False
return True
result = is_available_to_order(shop_menus, shop_orders)
print(result)
# 튜터님 풀이
def is_available_to_order(menus, orders):
menus_set = set(menus)
for order in orders:
if order not in menus_set:
return False
return True
result = is_available_to_order(shop_menus, shop_orders)
print(result)Comment : 파이썬에서 List를 Set으로 집합화 하는 이유가 in 연산자 때문이라는 것을 처음 알게되었습니다. in 연산자는 어떤 자료형을 탐색하느냐에 따라 시간복잡도의 차이가 발생합니다.
List는 in 연산을 O(N)의 시간복잡도로 처리합니다.
Set은 in 연산을 O(1)의 시간복잡도로 처리합니다. (최악의 경우 O(N)이긴 하지만, 매우 드문 경우로써 hash 구조로 작성된 데이터의 값이 모두 동일할때 발생)
https://twpower.github.io/120-python-in-operator-time-complexity
[Python] 파이썬 'in' 연산자 시간 복잡도(Time Complexity)
Practice makes perfect!
twpower.github.io
▶ 더하거나 빼거나
# 나의 풀이
numbers = [1, 1, 1, 1, 1]
target_number = 3
target_cnt = 0
def get_count_of_ways_to_target_by_doing_plus_or_minus(array, target, array_sum, index):
if index == len(array):
if array_sum == target:
global target_cnt
target_cnt += 1
return
get_count_of_ways_to_target_by_doing_plus_or_minus(array, target, array_sum + array[index], index + 1)
get_count_of_ways_to_target_by_doing_plus_or_minus(array, target, array_sum - array[index], index + 1)
get_count_of_ways_to_target_by_doing_plus_or_minus(numbers, target_number, 0, 0) # 5를 반환해야 합니다!
print(target_cnt)
# 튜터님 풀이
numbers = [2, 3, 1]
target_number = 0
result = [] # 모든 경우의 수를 담기 위한 배열
def get_all_ways_to_by_doing_plus_or_minus(array, current_index, current_sum, all_ways):
if current_index == len(array): # 탈출조건!
all_ways.append(current_sum) # 마지막 인덱스에 다다랐을 때 합계를 추가해주면 됩니다.
return
get_all_ways_to_by_doing_plus_or_minus(array, current_index + 1, current_sum + array[current_index], all_ways)
get_all_ways_to_by_doing_plus_or_minus(array, current_index + 1, current_sum - array[current_index], all_ways)
get_all_ways_to_by_doing_plus_or_minus(numbers, 0, 0, result)
print(len([value for value in result if value == target_number]))
# current_index 와 current_sum 에 0, 0을 넣은 이유는 시작하는 총액이 0, 시작 인덱스도 0이니까 그렇습니다!
# 그냥 result를 출력할 경우, 모든 경우의 수가 출력됩니다!
# [6, 4, 0, -2, 2, 0, -4, -6]Comment : 재귀함수의 사용법에 대해 다시한번 되새길 수 있었습니다.
5. 2주차 강의를 통해 새롭게 알게된 점
그동안 흐릿하게 알고 있었던 링크드 리스트와 배열의 차이점에 대해 보다 명확하게 이해할 수 있는 시간이었습니다.
또한 이진 탐색과 재귀의 개념에 대해 좀 더 명확하게 이해할 수 있었습니다.
'All Development' 카테고리의 다른 글
| Sparta_algorithm_course_04) velog (1) | 2022.07.23 |
|---|---|
| Sparta_algorithm_course_03) velog (0) | 2022.07.14 |
| Sparta_algorithm_course_01) velog (0) | 2022.06.30 |
| Unity) ML-Agents (0) | 2022.03.16 |
| Unity) Dotween (닷트윈) (0) | 2022.03.09 |